Resources

N/A

The recent acquisition of high fidelity computational resources at NASA Ames allows for the use of a mid-range Linux cluster for data mining and machine learning research. It is comprised of 16 slave nodes each containing two, quad-core Intel Xeon processors totaling 128 cores and 128GB RAM. For users that frequently run computationally intensive jobs within MATLAB, tapping the power of the cluster can greater reduce their computing time. They can easily access the cluster using the MATLAB distributed engine via the Distributed Toolbox.

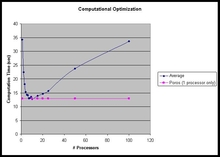
Recently, empirical results were generated to investigate the fidelity of these computational resources by constructing an experiment that varied the number of processors used in the cluster for a job consisting of 100 tasks. Each task contains multiple calls to multivariate Gaussian cumulative distribution function probability computations, which amounts to Monte Carlo evaluations of definite integrals over predefined hyper-rectangles. The job is instantiated by creating a simple for loop, with each pass through the loop representing a single task. Using the MATLAB job scheduler via available functions within the Distributed Computing Toolbox, these tasks were distributed over a number of processors ranging from 1 to 100. A baseline execution of the job was also run on the master node of the cluster, using only a single processor for comparison.

Various implementations of the algorithm performing the fundamental computation exist. The original implementation has been authored by Alan Genz, who makes his MATLAB source code publicly available, and makes use of various transformations so as to increase efficiency of the enabling Monte Carlo integration [1]. The results of running this particular version are shown in the last sheet of the spreadsheet attached to this website below, entitled “Un-Mex'd Mvnormcdf funct calls.” A second implementation has become available in the more recent versions of the Statistics toolbox within MATLAB, which are based in part upon Alan Genz’s algorithms. As such, this particular implementation is on par with the computation time of Genz’s original MATLAB implementation. Several years ago, a C-mex function was written by the author of this topic page, based completely upon Genz’s original implementation. The compiled mex function greatly increases the computational efficiency of the code in the loop by a ratio of about 123:1, as compared to Genz’s original implementation, without any use of distributed computing. The results of running this implementation with distributed computing compared to the baseline single processor case are shown in the second sheet of the spreadsheet attached to this website below, entitled “Mex'd Mvnormcdf function calls.”

The results in the last sheet indicate that the use of distributed processing greatly reduces computation time as the number of processors is increased when using Genz’s original implementation. The characteristic hyperbolic shape of the curve may be explained by the overhead encountered due to the increased communication required by the scheduler to manage the increasing number of processors for the submitted job. This same explanation can be used to interpret the results presented in the second sheet. These results indicate that the use of distributed processing has a local optimum for the number of processors when using the analogous C-mex routine. Interestingly, this local optimum appears to provide no additional computational advantage over running the exact same job with a single processor. Overall, the conclusion that can be drawn from these results is to provide information to data mining researchers about the pitfalls of using MATLAB’s Distributed Computing toolbox with mex files. Otherwise, for routines that have not already been optimized for computational efficiency via conversion into mex functions, distributed computing should be a natural choice. However, for this particular investigation, the absolute scale used to compare all implementations indicates that the use of the mex function on a single processor will yield as good a performance as any of the other implementations using distributing computing. We caution the reader that this may not always be the case for all routines, as the nature of the routine itself (looping involved, etc.) may have biased the results shown here.

[1] Alan Genz. Numerical computation of multivariate normal probabilities. Journal of Computational and Graphical Statistics, 1:141–149, 1992.

Attachments